Дилемма заключенных: you are (not) alone

Недавно прочитал пост о диллемме заключенных, который заинтересовал сообщество. Я согласен с написанным и считаю, что это хорошая работа, особенно учитывая, что автор школьник.
В данном посте хочу показать взгляд на эту проблему со стороны теории игр, на основе опыта полученного после обучения на онлайн курсах ИИ университета в Беркли. После применения данного аппарата проблема становится понятной и разрешимой.

Если построить дерево решений, то получится следующая схема:

где Я и ОН это заключенные
красные линии означают дачу показаний против другого заключенного
зеленые линии молчание
A, B, C, D — четыре возможных исхода
А — оба дают показания
B — я даю показания, он молчит
C — я молчу, он дает показания
D — мы оба молчим

Теперь зададим функцию выигрышей:
Для меня функция будет ровняться f1 = -m
Для него будет равняться f2 = -n

где m и n — количество получаемый лет заключения, мои и его соответственно, функции взяты с отрицанием, так как мы хотим сидеть за решеткой меньше
здесь m и n не зависимые переменные, так как у нас игра с не нулевой суммой, иначе функции выглядели бы так:
Для меня f1 = -m
Для него f2 = m
здесь второй заключенный стремится чтобы мы сидели дольше и пытается максимизировать m.

Возьмем для примера данные с вики про возможные исходы, тогда:
A = -2;- 2
B = 0;- 10
C = -10; 0
D = -1; -1
где первое и второе число, выигрыш мой и его соответственно
Получим следующую схему, которую нам нужно решить:

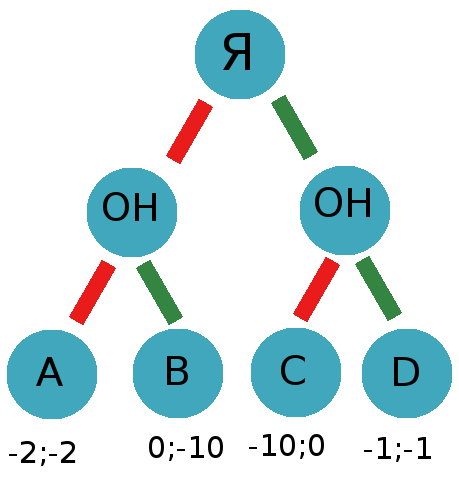
Теперь попробуем разрешить данную проблему и решить какой ход нам сделать. Сначала попробуем алгоритм minimax, который в нашем случае будет в виде maximax, так как оба игрока пытают максимизировать свой выигрыш. Получаем следующий результат:

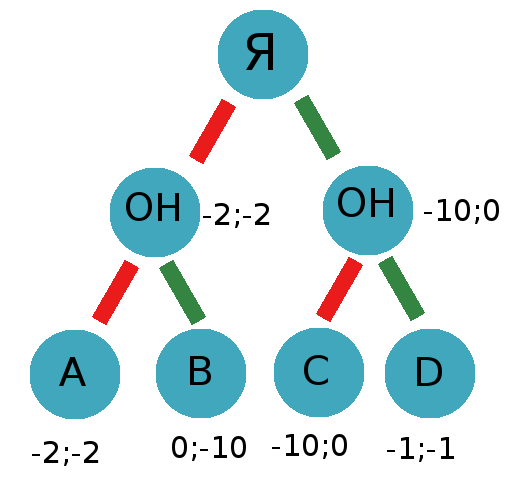
Как мы видим второй игрок будет всегда предавать, так как старается максимизировать свой выигрыш. Я должен тоже выбрать предательство — исходя из той же причины.

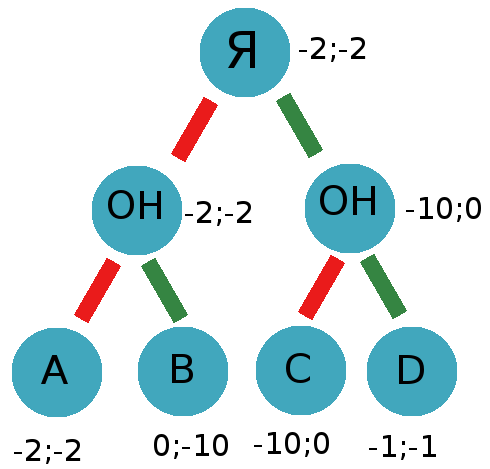
Данный алгоритм максимакс плохо работает в реальном мире, так как всегда настроен на плохой исход. В таких ситуациях значительно лучше себя показывает алгоритм ожидаемого максимума(expectimax). Этот алгоритм учитывает, что игроки могут выбирать не самые выгодные для себя ходы.
Допустим, что ОН предает в 50% случаев, тогда:
выигрыш нашего предательства будет равен 0.5*(-2) + 0.5*(0) = -1
выигрыш нашего молчания 0.5*(-10) + 0.5*(-1) = -5.5
или тоже самое на схеме:

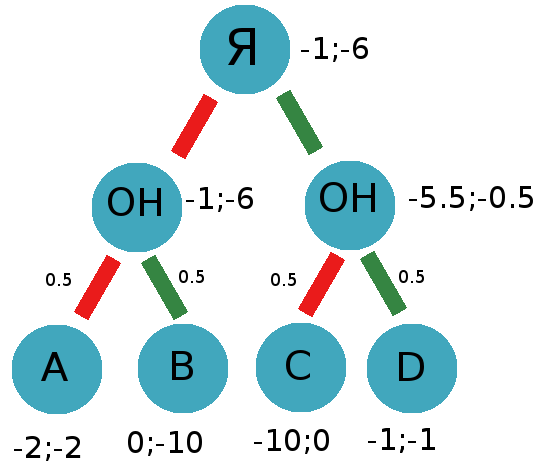
Как видно, даже с более подходящим алгоритмом чуда не произошло и нам все также выгоднее предавать. Даже если вероятность ЕГО молчания увеличится все равно при данных условиях выгоднее предавать. Если мы будем знать что ОН всегда будет молчать мы выберем предательство.

Почему так? Где мы просчитались?
Мы забыли рассмотреть одну очень важную деталь — функцию выигрышей. А что если нам не безразлична ЕГО судьба, а ему не безразлична НАША? Тогда функции выигрышей будут такими:
f1 = -m -n
f2 = -m -n
где m и n — количество получаемый лет заключения, мои и его соответственно
Тогда получаем следующую схему:

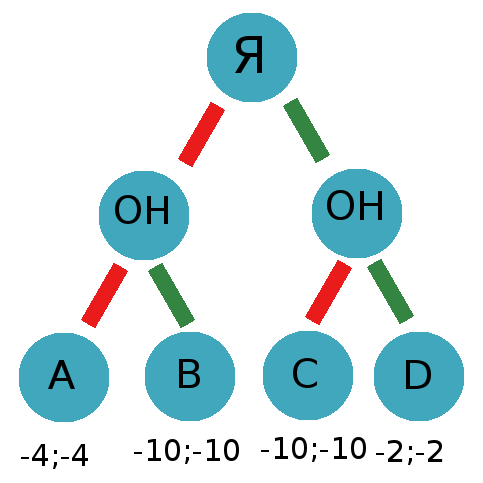
и теперь все кардинально меняется, для максимакса решение для МЕНЯ получится молчать, так как Я буду выбирать между -4;-4 слева(предательство) и -2;-2 справа(молчание)
а для ожидаемого максимума с 50% ЕГО предательства получится:
для моего предательства выигрыш -7
для моего молчания выигрыш -6
Следовательно — молчим.
Внимательный хабраюзер заметит, что если вероятность ЕГО предательства будет возрастать, то для МЕНЯ будет уже выгоднее предавать.

Как же узнать эти вероятности — на основе предыдущего опыта.
Допустим ОН раньше в 9 случаях из 10 молчал, следовательно ставим ему вероятность предательства 10%
Правда в реальном мире эти вероятности зависят от большого количества факторов и найти их является одной из основных проблем.

Так же стоит помнить что функции выигрышей могут иметь другой вид, более эгоистичный, например:
f1 = -m/2 — n
здесь мы помним про НЕГО, но все равно если будет выбор между ЕМУ сидеть 1 год или МНЕ 2, Я предпочту второй вариант.
Эту функцию тоже сложно найти.

Вывод:

Я считаю что дилемма заключенных это дилемма недостаточных входных данных. Если мы будем знать с какой вероятностью ОН предаст, как МЫ эгоистичны и как эгоистичен ОН, то сможем принять решение очень близкое к верному.